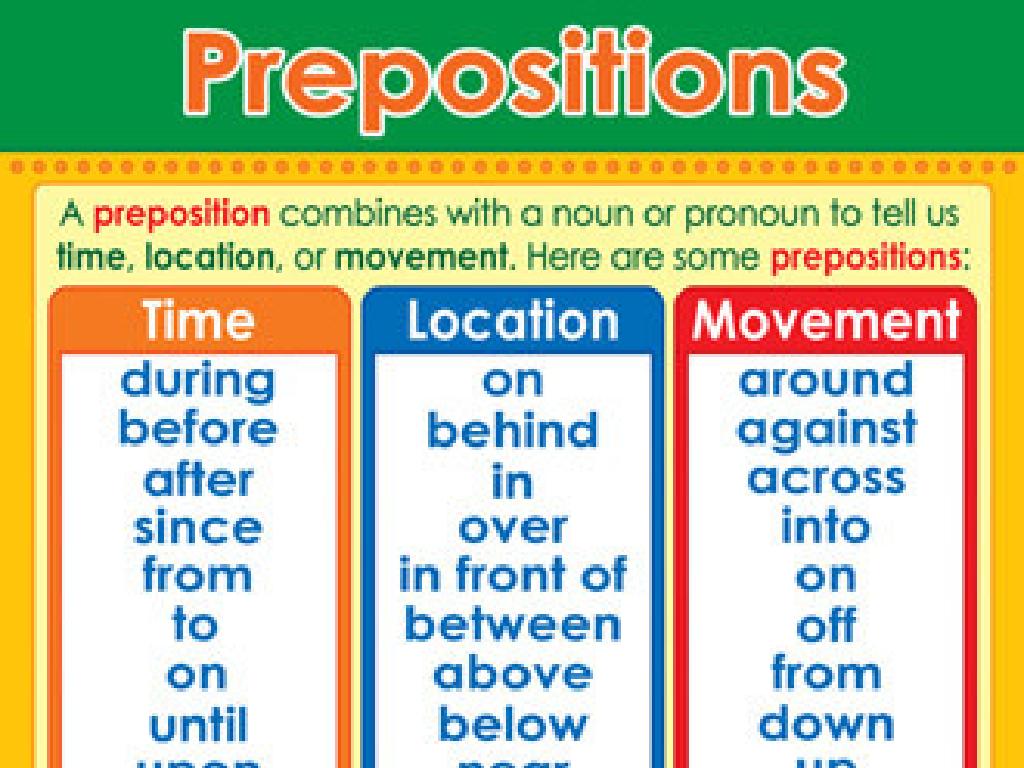
Least Common Denominator
Subject: Math
Grade: Sixth grade
Topic: Fractions And Decimals
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Understanding the Least Common Denominator
– Grasping the basics of fractions
– Fractions represent parts of a whole
– Defining the denominator
– The bottom number of a fraction, showing how many equal parts the whole is divided into
– Importance of the LCD
– LCD helps us combine fractions with different denominators
– Practical uses of LCD
|
This slide introduces the concept of the least common denominator (LCD) as part of understanding fractions. Begin by explaining fractions as parts of a whole, which is crucial for grasping how they operate. Clarify that the denominator is the bottom number of a fraction and indicates the total number of equal parts. Emphasize the importance of the LCD in adding, subtracting, and comparing fractions with different denominators. Illustrate with examples how finding the LCD allows for the combination of these fractions into a single expression or comparison. Encourage students to think of situations where combining fractions might be necessary, such as in cooking or dividing a set of items, to understand the practical applications of LCD.
Identifying Denominators in Fractions
– Denominator: bottom number in a fraction
– Examples: denominators in daily life
– Pizza slices (1/8), weekly allowance (1/7), or measuring cup (1/4)
– Finding common denominators
– Common denominators are used to compare or add fractions
– Least common denominator (LCD)
– The smallest number that all denominators can divide into
|
This slide introduces the concept of denominators as part of a fraction, which is crucial for understanding how to compare and work with fractions. Start by explaining that the denominator represents the total number of equal parts in a whole. Use everyday examples to illustrate denominators, such as slices of pizza or days in a week. Then, guide students through the process of finding common denominators, which is necessary for adding, subtracting, or comparing fractions. Emphasize the importance of the least common denominator (LCD) as it simplifies calculations and helps in solving fraction problems more efficiently. Provide practice problems where students can find the LCD and use it to perform operations with fractions.
Understanding the Least Common Denominator
– Define Least Common Denominator (LCD)
– The smallest common multiple of the denominators of two or more fractions.
– Importance of finding LCD
– LCD is essential for adding, subtracting, or comparing fractions effectively.
– LCD in real-life scenarios
– Used in recipes, construction, and time management to combine different measurements.
– Practice finding LCD
|
The Least Common Denominator (LCD) is a foundational concept in working with fractions. It refers to the smallest number that is a common multiple of the denominators of two or more fractions. Understanding LCD is crucial for performing addition and subtraction of fractions, as it allows for a common basis for comparison. In real-life, LCD is used in various situations such as adjusting recipes, combining different lengths in construction, or managing activities that take different amounts of time. This slide will introduce students to the concept of LCD, explain its importance, and show how it is applied in everyday life. Encourage students to practice finding the LCD by presenting them with fractions that have different denominators and guiding them through the process of identifying the smallest common multiple.
Finding the Least Common Denominator (LCD)
– List multiples of denominators
– For 1/2 and 1/3, list 2’s multiples (2, 4, 6, 8…) and 3’s (3, 6, 9, 12…)
– Spot the common multiples
– Look for multiples that appear in all lists. For 1/2 and 1/3, it’s 6, 12…
– Select the smallest common multiple
– The smallest number in all lists is the LCD. For 1/2 and 1/3, the LCD is 6
|
When teaching how to find the LCD, start by explaining the importance of having a common denominator for adding or subtracting fractions. Demonstrate listing multiples by using simple denominators like 2 and 3. Encourage students to identify common multiples from the lists they create. Emphasize the selection of the smallest common multiple, as this is the LCD needed to compare, add, or subtract fractions. Provide additional examples with different denominators and possibly higher numbers to ensure understanding. Allow students to practice with pairs or small groups to find the LCD for various sets of fractions.
Finding the Least Common Denominator (LCD)
– LCD for 1/4 and 1/5
– Multiply denominators: 4 * 5 = 20, so LCD is 20
– LCD for 2/3 and 3/8
– Multiply denominators: 3 * 8 = 24, find multiples until common one is found
– Steps to find LCD
– List multiples of denominators, find smallest common multiple
|
This slide provides examples to demonstrate the process of finding the least common denominator (LCD) for different sets of fractions. In Example 1, we multiply the denominators (4 and 5) to find the LCD, which is 20. In Example 2, we multiply the denominators (3 and 8) to get 24, but we must also list the multiples of each denominator to find the smallest common multiple, which is the LCD. The steps taken include listing multiples of each denominator and identifying the smallest number that appears in both lists. This method ensures that students understand the concept of LCD and can apply it to add or subtract fractions with different denominators.
Practice: Finding the Least Common Denominator
– Problem 1: LCD for 1/6 and 1/9
– Multiply denominators, then find smallest number both divide into
– Problem 2: LCD for 5/12 and 3/4
– Factor each denominator, then find smallest common multiple
|
This slide is designed for a class activity where students will practice finding the least common denominator (LCD) for pairs of fractions. For Problem 1, guide students to multiply the denominators (6 and 9) and then find the smallest number that both 6 and 9 can divide into evenly, which is 18. For Problem 2, instruct students to factor each denominator into its prime factors (12 = 2^2 * 3 and 4 = 2^2), then find the smallest common multiple of these factors, which is 12. Encourage students to work through these problems step-by-step and to check their work by ensuring the fractions with the new denominator are equivalent to the original fractions. Provide additional examples if time allows and encourage peer discussion to facilitate learning.
Class Activity: LCD Scavenger Hunt
– Find items with fractional labels
– Pair up to calculate LCDs
– Use different sets of fractions to find the least common denominator
– Discuss LCD finding strategies
– How did you determine the LCD for each set?
– Share results with the class
|
This interactive activity is designed to help students apply their knowledge of least common denominators (LCD) in a fun and engaging way. Students will search for items around the classroom or school that have fractional labels. Working in pairs, they will list the fractions and find the LCD for each set. Encourage them to discuss their strategies for finding the LCD. After the activity, students will share their answers and methods with the class, allowing for collaborative learning. Possible variations of the activity could include using fractions from recipes, craft instructions, or measurements found in the school environment. The goal is to reinforce the concept of LCD in various contexts and to enhance problem-solving skills.
Wrapping Up: Least Common Denominator
– Recap: What is LCD?
LCD is the smallest number that two or more denominators can divide into.
– Why master LCD?
Understanding LCD is crucial for adding, subtracting, and comparing fractions.
– Homework: 10 LCD Challenges
Find the LCD for 10 different pairs or sets of fractions and show your work.
– Practice makes perfect!
|
As we conclude today’s lesson, remember that the Least Common Denominator (LCD) is the smallest common multiple of two or more denominators. Mastering the concept of LCD is essential for performing operations with fractions effectively, such as adding and subtracting fractions with different denominators, as well as comparing fractions. For homework, students are expected to find the LCD for 10 different sets of fractions, which will reinforce their understanding and provide practice in identifying multiples. Encourage students to explain their thought process for each set, as this will help solidify their grasp of the concept. During the next class, we can review some of the homework examples to ensure everyone is confident with the process.