Your next great Lessn starts here.

Welcome to Multiplication! – Greetings, young mathematicians! – Let’s review what multiplication is – Multiplication is adding a number repeatedly – Discover rules that simplify multiplying – We’ll explore properties like Commutative, Associative, and Distributive – Get ready for some multiplication magic! | Begin the class with a warm welcome to set a positive tone for learning. Quickly review the concept of multiplication as repeated addition to ensure all students are on the same page. Introduce the idea that there are special rules in multiplication, known as properties, which can make calculations easier and faster. These properties are tools that can help solve multiplication problems more efficiently. Emphasize that understanding these rules is like learning magic tricks that can make numbers work for us in amazing ways. Prepare to engage the students with examples and interactive activities that illustrate these properties in action.

Understanding Properties of Multiplication – What is a ‘property’ in math? – A rule that is always true for numbers – Importance of properties in multiplication – Helps solve multiplication problems faster – The Commutative Property – Order doesn’t change the product: 3 x 4 = 4 x 3 – The Associative & Distributive Properties – Grouping (Associative) and breaking apart (Distributive) numbers can make multiplying easier | This slide introduces the concept of mathematical properties and their significance in multiplication. A property is a rule that always applies to numbers, and understanding these can greatly simplify multiplication problems. The Commutative Property states that the order of numbers does not affect the product, while the Associative Property allows us to group numbers differently without changing the result. The Distributive Property lets us break down a multiplication problem into smaller, more manageable parts. Emphasize these properties with examples and encourage students to apply them in practice problems to see how they make multiplication easier and more efficient.

The Commutative Property of Multiplication – Understanding Commutative Property – Commutative Property: a x b = b x a – Examples: Switching numbers – For instance, 3 x 4 = 4 x 3 = 12 – Order doesn’t change the product – Whether 5 x 2 or 2 x 5, the answer is 10 | This slide introduces the Commutative Property of Multiplication, which states that the order in which two numbers are multiplied does not affect the product. Use simple number examples to illustrate this property, such as 3 x 4 and 4 x 3 both equaling 12. Emphasize that this rule helps in making multiplication easier, as students can choose the order of factors that makes the multiplication simpler for them to compute. Encourage students to try this with different numbers and verify that the product remains the same, reinforcing their understanding through practice.

The Associative Property of Multiplication – Understanding Associative Property – (a x b) x c = a x (b x c) means the way numbers are grouped doesn’t change the total. – Numerical example demonstration – For example, (2 x 3) x 4 = 2 x (3 x 4) both equal 24. – Grouping doesn’t affect product – Whether you group the first two numbers or the last two, the answer is the same. | The Associative Property of Multiplication states that the way in which factors are grouped does not affect the product. This property allows for flexibility in computation and simplifies calculations. When teaching this concept, use clear numerical examples to show that no matter how the numbers are grouped, the product remains unchanged. Emphasize that this property only works with multiplication (and addition), not with subtraction or division. Encourage students to practice with different sets of numbers to reinforce the concept.

The Distributive Property of Multiplication – Understanding the Distributive Property – a x (b + c) is the same as (a x b) + (a x c) – Multiplication distributes over addition – For example, 3 x (2 + 4) equals (3 x 2) + (3 x 4) – Examples of the Distributive Property – See how 3 x 6 breaks down into (3 x 2) + (3 x 4) – Simplifying larger problems – Break down tricky problems into smaller, easier steps | 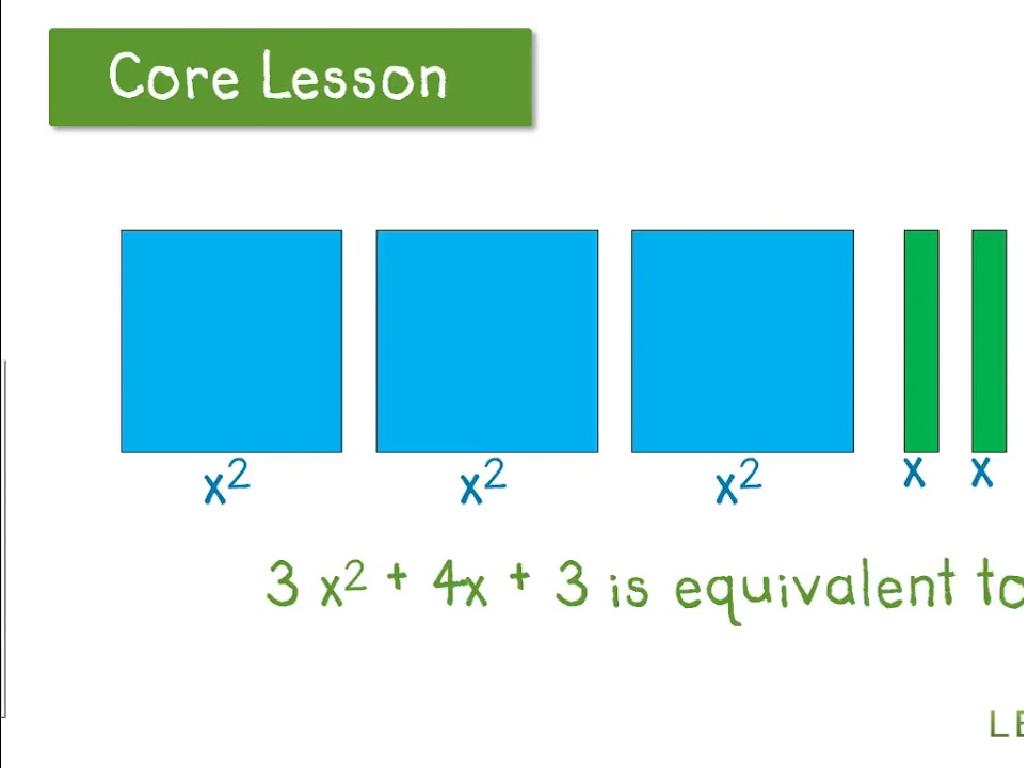The Distributive Property allows us to multiply a number by a group of numbers added together. It’s like handing out or ‘distributing’ the multiplication to each addend within the parentheses. For instance, if we have 3 x (2 + 4), we can distribute the 3 to both 2 and 4, making it (3 x 2) + (3 x 4), which simplifies to 6 + 12, and finally to 18. This property is especially useful for solving larger multiplication problems by breaking them into smaller, more manageable pieces. Encourage students to practice this property with different numbers to become comfortable with the concept.

Properties in Action: Complex Example – Review all multiplication properties – Step-by-step complex example – Example: Calculate 4 x (6 x 25) using properties – Identify properties used in steps – Which property applies to each calculation step? – Encourage student participation – Ask students to volunteer answers | This slide aims to consolidate the students’ understanding of the properties of multiplication by applying them to a complex example. Begin by reviewing the properties learned: commutative, associative, and distributive. Work through a complex example such as 4 x (6 x 25), breaking it down step by step. At each step, pause to ask the students which property is being used and why. This interactive approach helps students to actively engage with the material and reinforces their understanding. Encourage students to participate by volunteering to identify the properties and explain their reasoning. This will not only help them to remember the properties but also to understand how they can be applied to simplify multiplication problems.

Practice Time: Multiplication Properties – Distribute practice worksheets – Apply the right multiplication property – Use commutative, associative, or distributive property – Discuss solutions with classmates – Talk about how you solved the problems – Collaborate to solve problems – Work together to find answers | This slide is to guide the students through a hands-on practice activity. Distribute worksheets with a variety of multiplication problems that require the use of different properties of multiplication. Encourage students to identify whether they should use the commutative, associative, or distributive property to solve each problem. Promote peer discussion to allow students to explain their thought process and reasoning. This collaborative approach not only helps students learn from each other but also reinforces their understanding of the concepts. As a teacher, walk around the classroom to facilitate discussions, provide guidance, and ensure that each student is engaged in the activity. Prepare to offer hints or further explanation as needed.

Class Activity: Multiplication Bingo – Introduction to Multiplication Bingo – Distribute bingo cards with products – Each card has different multiplication answers – Call out multiplication expressions – Solve the problems as they are called out – Mark the product and aim for Bingo! – First to get five in a row shouts ‘Bingo!’ | This interactive class activity is designed to help students practice their multiplication skills in a fun and engaging way. Begin by explaining the rules of Multiplication Bingo. Each student will receive a bingo card filled with products of multiplication problems. As the teacher, you will call out multiplication expressions, and students will need to quickly solve them and mark the corresponding product on their bingo cards. The first student to get five correct products in a row, either horizontally, vertically, or diagonally, wins the game. Prepare different bingo cards to ensure a variety of winners. Encourage students to double-check their answers before shouting ‘Bingo!’. This activity not only reinforces multiplication facts but also promotes active listening and concentration.

Wrapping Up: Multiplication Properties – Recap multiplication properties – Commutative, Associative, Distributive, Identity, and Zero properties – Share your thoughts – What did you enjoy learning? What was tough? – Practice makes perfect – Keep exploring at home – Use the exercises to become a multiplication master | As we conclude today’s lesson, it’s important to review the properties of multiplication: commutative, associative, distributive, identity, and zero. Encourage students to reflect on what they found interesting or challenging about these concepts. Remind them that understanding these properties will make solving multiplication problems easier. Provide students with practice exercises to complete at home, reinforcing the day’s learning. Encourage them to explore these properties further with real-life examples and to come back with any questions for the next class.