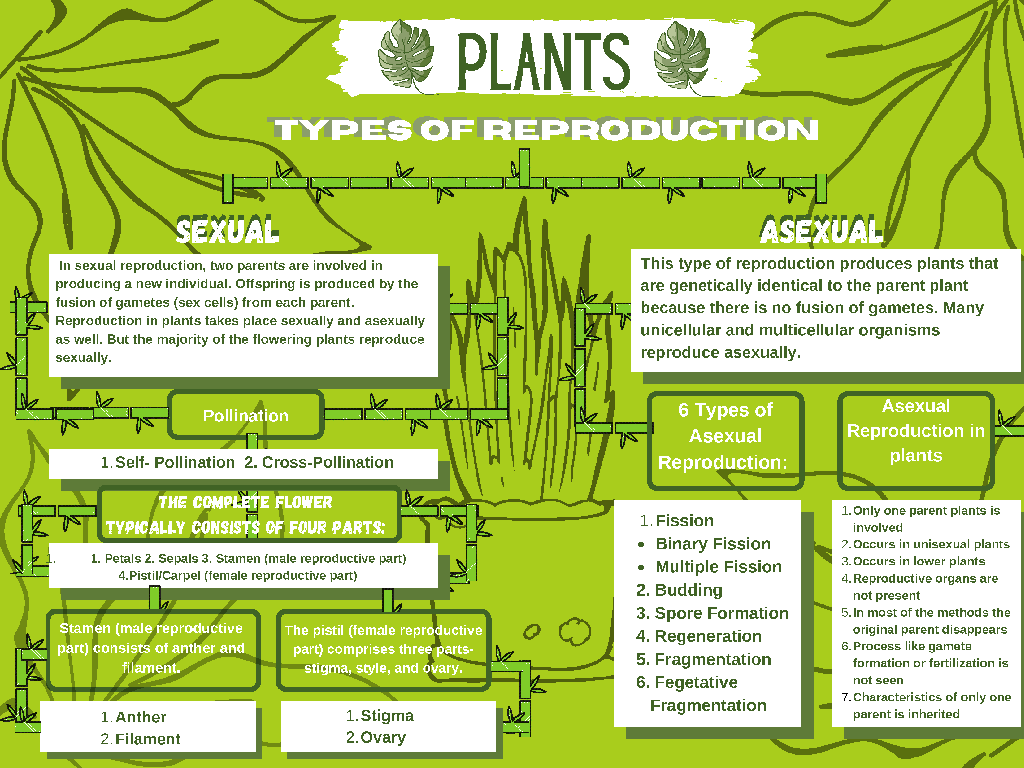
Identify Proportional Relationships By Graphing
Subject: Math
Grade: Seventh grade
Topic: Proportional Relationships
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Understanding Proportional Relationships
– Proportions in everyday life
– Ratios that remain constant, like recipe ingredients
– Defining proportional relationships
– Two quantities increase/decrease at the same rate
– Real-world proportional examples
– Examples: speed/distance, price/quantity
– Graphing proportions
– Plotting points on a graph to see the constant ratio
|
This slide introduces the concept of proportional relationships, a fundamental aspect of mathematics that students encounter in various real-life situations. Begin by discussing how proportions are present in everyday scenarios, such as in cooking recipes where ingredients are mixed in a fixed ratio. Explain that a proportional relationship is when two quantities increase or decrease at the same rate, maintaining a constant ratio. Provide relatable examples such as the relationship between speed and travel time, or the cost of an item and its quantity. Finally, illustrate how these relationships can be graphed, showing a straight line through the origin, which visually represents the constant ratio. Encourage students to think of other examples and to practice graphing proportional relationships to solidify their understanding.
Understanding Proportions in Graphs
– Define a proportion
– A proportion is an equation stating two ratios are equivalent.
– Significance of the ‘equals’ sign
– The ‘equals’ sign indicates that two quantities are the same in value.
– Simple proportion examples
– For instance, 1/2 = 2/4 or 3/6 is a simple proportion.
– Graphing proportional relationships
– When graphed, proportional relationships form a straight line through the origin.
|
This slide introduces the concept of proportion, which is a cornerstone in understanding relationships between quantities in math. Emphasize that a proportion is an equation that shows two ratios are equivalent, and the ‘equals’ sign is a symbol of that equivalence. Use everyday examples to illustrate simple proportions, such as recipes or similar geometric shapes. When it comes to graphing, explain that proportional relationships will always create a straight line that passes through the origin (0,0), which visually represents the constant rate of change. Encourage students to think of real-life examples where proportions are used and to practice graphing these relationships to solidify their understanding.
Graphing Proportional Relationships
– Understand X and Y axes
– X-axis is horizontal, Y-axis is vertical
– Learn to plot points
– Each point is a pair (x, y) on the graph
– How to read graph values
– Find the value by locating the point and reading across and down
– Recognize proportional graphs
– Straight line through the origin (0,0) shows proportionality
|
This slide introduces students to the fundamental concepts of graphing as a precursor to understanding proportional relationships. Begin by explaining the layout of a graph with the X (horizontal) and Y (vertical) axes. Demonstrate how to plot points on the graph using ordered pairs (x, y). Show how to read values from a graph by finding the point and looking at the corresponding values on both axes. Emphasize that a proportional relationship on a graph will be represented by a straight line that passes through the origin (0,0). Provide examples of proportional and non-proportional graphs for comparison. Encourage students to practice plotting points and identifying proportional relationships in class activities.
Graphing Proportional Relationships
– Visual traits of proportionality
– Straight line through the origin (0,0)
– Understanding constant ratios
– Constant ratio means the y/x value remains the same
– Steps to graph proportional relationships
– Plot points, check for straight line through origin
– Practice with real examples
– Use examples like speed vs. time, or recipe ingredient adjustments
|
This slide introduces students to the concept of proportional relationships in a graphical context. Begin by explaining that a proportional relationship between two variables will appear as a straight line through the origin on a graph. Emphasize the concept of a constant ratio, which is the foundation of proportionality, meaning for every x there is a consistently multiplied y. Demonstrate the steps to graph proportional relationships: choosing values, plotting points, and checking if the graph is a straight line through the origin. Provide real-life examples such as the relationship between speed and time or scaling ingredients in a recipe to solidify understanding. Encourage students to practice by creating their own graphs with given ratios.
Characteristics of Proportional Graphs
– Proportional graphs are straight lines
– They pass through the origin (0,0)
– The point where x and y axes meet
– These lines have a constant slope
– Slope (rise over run) remains the same
– Real-world examples of proportionality
– E.g., speed vs. time, recipe ingredient ratios
|
This slide aims to help students identify proportional relationships by looking at their graphical representations. Emphasize that proportional graphs will always be straight lines, indicating a consistent rate of change. The fact that these lines pass through the origin (0,0) is a key characteristic that students should be able to recognize. Discuss the concept of slope as a measure of this rate of change, and ensure students understand that it remains constant in proportional relationships. Provide real-world examples to illustrate these concepts, such as the relationship between speed and time during constant motion, or the ratios of ingredients in a recipe. Encourage students to think of other examples and to practice graphing proportional relationships.
Practice Time: Graphing Proportional Relationships
– Let’s plot points on a graph
– Determine if relationships are proportional
– Two variables are proportional if they maintain a constant ratio.
– Share and discuss your graphs
– Explain your reasoning for the relationships shown.
– Reflect on the exercise
– What did you learn from this graphing activity?
|
This slide is designed for a hands-on graphing activity to help students identify proportional relationships. Start by plotting points on a graph together as a class. Then, guide students to determine if the relationships between the variables are proportional by checking if they maintain a constant ratio or rate. Encourage students to share their graphs with the class to foster a collaborative learning environment. Discuss the different graphs and reasoning behind the proportional or non-proportional relationships identified. Conclude the activity by reflecting on what was learned and how this skill applies to real-world scenarios. Possible activities include graphing time versus distance for different speeds, money saved over time, or quantities in recipes. These examples will help students grasp the concept of proportionality in a tangible way.
Class Activity: Graphing Proportional Relationships
– Select a proportional relationship
– Graph the relationship on a coordinate plane
– Use a ruler for straight lines, plot points accurately
– Explain why you chose this relationship
– Discuss the real-life relevance or interest in the relationship
– Share your graph with the class
|
This activity is designed to help students apply their understanding of proportional relationships by creating their own graphs. Students should think of a relationship where one quantity changes at a constant rate with respect to another, like speed and time, or cost and quantity. They will then graph this relationship, ensuring that the points form a straight line through the origin, which indicates proportionality. Encourage students to explain their choice, focusing on how the relationship shows proportionality. Possible activities: 1) Graphing distance vs. time for a car traveling at a constant speed. 2) Graphing the total cost vs. number of items bought at a unit price. 3) Graphing the amount of ingredients vs. servings in a recipe. 4) Graphing the height of a plant over time if it grows at a constant rate. 5) Graphing the amount of money saved over time with a fixed weekly saving. After graphing, students should present their graph and explanation to the class, fostering a discussion on how different proportional relationships can be represented visually.
Conclusion: Proportional Relationships by Graphing
– Recap on graphing proportions
– Remember: straight line through the origin
– Significance of proportions
– Used in recipes, map reading, and more
– Time for Q&A
– Review homework assignment
– Practice with provided problems
|
As we wrap up today’s lesson, let’s review the key concept of identifying proportional relationships through graphing. Remember, a proportional relationship between two variables will always be represented by a straight line that passes through the origin on a graph. Understanding proportions is crucial as it applies to real-life situations like adjusting recipes, reading maps, or scaling models. Now, let’s open the floor for any questions you might have. It’s important to clarify doubts now to solidify your understanding. Lastly, please complete the assigned homework problems to practice graphing proportional relationships. This will help reinforce today’s lesson and prepare you for the next class.